Batch 3 - Class 210 - McGuire the Gathering
Pre-Class Exercise
Develop some algorithm for solving for lily pad farthest from the arm for the following pattern
- You can clear 3 arms as under. The pink ones stack up at 4, the orange ones at 5, and they in turn can jump to the lazy frog
- Similarly to clear 5 arms. Solve for the white ones to finish the solution.
Attendance Kabir, Vansh, Aashvi, Rhea, Arnav, Anishka, Rehaan, Anshi, SiddharthM, Kushagra
Class puzzles
You want to gather your clansmen for an impending war. You have one trusted servant who will go out and recruit for you. If you send him out for a five day journey, five clansmen will start to arrive on the fifth day and every day thereafter. You will win if your forces outnumber your opponent by 30 on any day.
Unfortunately, your opponent discovers that you are sending out your trusted man for five days. How many days will she send out her trusted servant, in order to defeat you? She could choose 10 days. Note that you have 25 more men on 9th day, but on day 10, that difference drops to 20, and then keeps decreasing. Your opponent defeats you on day 20!

What are some other numbers your opponent could choose?
Lets start again. What if you chose 10. What number could she choose?
- Does 15 beat 10?
- Any other numbers?
Is there any number that is unbeatable?
- Can you prove that?
This makes the game uninteresting, because the second person always wins. Lets make the game interesting. You put any number of numbers in a bag. Your opponent chooses a number by looking at that whole set. Then you pick a random number from the bag, and that's your number.
For example, if you put 5, 10, 11, 15 in the bag, what would you opponent do?
- She could choose 6, which beats 5, 11 and 15. Thus when you pick the random number, you have 3/4 chances of losing and 1/4 of winning.
- She could also choose 12, which beats 10, 11 and 15
- She could also choose one of the numbers you chose. For example, 5, 10 or 11 below (explain the chart to students - Arrow from 5 to 15 means that 5 beats 15)
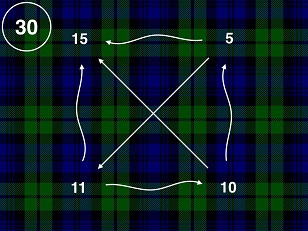
Your job is to choose numbers to put into the bag, so that your chances of winning are at least same as your opponent. Experiment as a class - one person chooses the numbers, and the rest of the class tries to beat those numbers by choosing a number. Instructor Note: This may take some time, let students experiment here.
- What if you chose 5, 10 and 11? The opponent could choose 6 or 12
- The only wining set is 6, 8, 10, 11, 12. Examine the solution to understand what is going on.
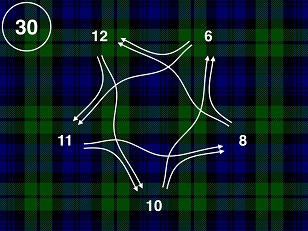
Note that this problem seems a bit like "Rock, Paper, Scissor". Many times, we are used to thinking of transitive properties in maths. If 3>2 and 4>3, then 4>2. However, many constructs are not transitive. Such as "Rock, Paper, Scissor". This problem is another example of a non-transitive structure. 12>10, 10>6 but 6>12 (note that ">" sign here means that 12 beats 10)
Battles could get bigger - instead of difference of 30 soldiers, you could need a difference of 50 or 100 soldiers. Can you try to arrive at some patterns?
- Start from smaller numbers - 1, 2, ... 10
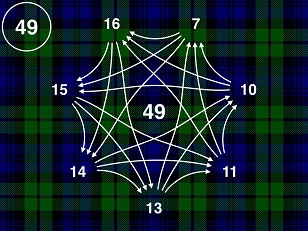
- Study the following solution for 49 and 50. What do you observe? What are some commonalities between the 30 solution and this?
.jpeg)
- Can you put even numbers into the bag? Why/ why not?
- Prove that any number in the bag must have equal number of wins/losses arrows
- Solution for 1-100. What patterns do you see
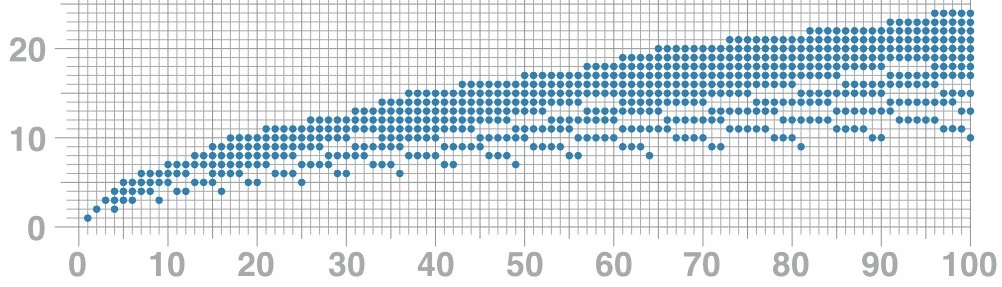
- Notice what happens at square numbers like 4, 9, 16
- Notice what happens at product of two consecutive numbers, like 12 (3x4), 20 (4x5)
- Notice what happens above a certain dot - it almost seems like a dot explodes into two, then into three and so on going upwards. And the horiontal distance between those successive vertical patterns goes on increasing
- The empty regions seem to be forming a pattern
- Draw the pattern on number of numbers in the bag for different solutions. The block sizes seem to increase by 8 everytime (34-60, which is a 27 size block, requires 8 numbers ; 61-95, 35 size block, requires 9 numbers ; and so on)
Homework
- What is the probability, if you roll a coin across a chessboard and it comes to rest on the board, that it covers some corner of one of the grid squares? (You can assume that the diameter of the coin is less than the sidelength of a single square on the chessboard.)
- Answer: If the radius of coin is r and side of square on chessboard is s, the coin will cover an intersection only if it is in the quarter circle around that intersection. Any given square has four such quarter circles. So area of coin/ area of square is the probability that the coin covers any intersection.
References: